Space for assignment 2.
I got some questions about the list via email. Unfortunately in Polish, if some of you care, please translate:
> mam pewne problemy ze zrobieniem zadania 2 z assigmentu 2. Próbuję rozpisać wzory na gradient kolejnych wyrażeń wykorzystując chain rule, obliczenie O2_grad jest dla mnie jasne, z tego co rozumiem taki gradient ma mieć taki sam kształt, jak O2, czyli jest macierzą Nx1. Następnie chcemy obliczyć A2_grad, z chain rule wiemy, że jest to O2_grad * (d O2 / d A2), z czym mam problem, ponieważ O2_grad ma kształt (N,1), a (d O2 / d A2) jest macierzą, w naszym przypadku rozmiaru NxN, niezależnie, czy mnożenie jest broadcastowane, czy jest mnożeniem macierzy nie da się go wykonać. Następnie chcąc obliczyć b2_grad widzę intuicyjnie, że wynik wynosi A2_grad.sum(0), ale nie potrafię tego uzasadnić za pomocą chain rule, ponownie mamy wyrażenie A2_grad (rozmiaru Nx1) * (d A2 / d b2) (nie wiem jakiego rozmiaru powinno być takie wyrażenie) i nie do końca wiem co zrobić, żeby otrzymać pojedyncza liczę równą A2_grad.sum(0). W przypadku W2_grad ciężko mi już intuicyjnie ustalić jak powinien wyglądać wynik, a powyższe problemy z rozumieniem chain rule uniemożliwiają mi zrobienie tego mechanicznie. Być może problemy wynikają z błędnego rozumienia obliczania gradientów, lub tego, jakiego rozmiaru i kształtu powinny być np. A2_grad lub (d A2 / d b2). Byłbym wdzięczny za wyjaśnienie / wskazówki na ten temat, w mailu lub na jutrzejszym wykładzie / konsultacjach.
Answer/comment
Math matrix notation assumes that functions take scalars or vectors, and return scalars or vectors. Then they have a well defined derivative (in: scalar, out: scalar), gradients (in: vector, out:scalar), or Jacobians (in:vector, out: vector). In deep learning, we frequently assume that functions (layers) take higher-order tensors and return them as well (e.g. a linear layer takes a minibatch of examples, i.e. a matrix, and returns a matrix as well). Such cases require extensions to the matrix notation for derivatives. I did't want to introduce one, because it makes it harder to see the gist of what we are doing.
Still, you need to solve the Assignment 2, which requires you to write an implementation for those higher order tensors. My usual take was to:
- Observe, that the loss
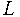 is a scalar, so we always have gradients
is a scalar, so we always have gradients - You can always compute partial derivatives (e.g. if
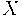 is a matrix, compute the derivative
is a matrix, compute the derivative 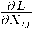 . Having the formula for one element of the backpropagated gradient, you can usually work out an appropriate numpy expression. Note that numpy is more versatile than matrix notation (you have broadcasting, you have reductions, etc.).
. Having the formula for one element of the backpropagated gradient, you can usually work out an appropriate numpy expression. Note that numpy is more versatile than matrix notation (you have broadcasting, you have reductions, etc.). To check the validity of your code, work out from the end. E.g. For Assignment 2: First, think about the lines
O2 = sigmoid(A2)
loss = -Y * np.log(O2) - (1-Y) * np.log(1.0 - O2)
loss = loss.sum() / X.shape[0]Can you compute A2_grad, which is defined to be
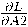 ? Start with A2 being a scalar, then try to compute the formula of the derivative, then write a function for it, then debug it with a gradient checker, then try to numpy-generalize it to work when A2 is a matrix.
? Start with A2 being a scalar, then try to compute the formula of the derivative, then write a function for it, then debug it with a gradient checker, then try to numpy-generalize it to work when A2 is a matrix.Then add the expression for computing A2 and add another line for the gradient, then expand it by one more equation...
Some examples of generalizing the derivative computation:
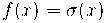 with the function applied elementwise whenever
with the function applied elementwise whenever 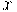 is not a scalar. Then the derivative is also computed elementwise:
is not a scalar. Then the derivative is also computed elementwise: 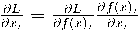
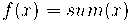 then
then 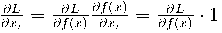
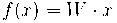 with
with 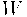 ,
, 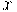 matrices. Then
matrices. Then 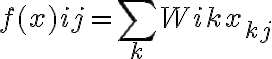 and
and 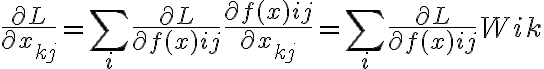 , then when you try to write a single numpy formula that computes the whole matrix of pertial erivatives wrt x you will get another matrix multiplication...
, then when you try to write a single numpy formula that computes the whole matrix of pertial erivatives wrt x you will get another matrix multiplication...
